Tổng hợp các đề toán thực tế ôn thi tuyển sinh 10 năm 2025 có lời giải?

Tổng hợp các đề toán thực tế ôn thi tuyển sinh 10 năm 2025 có lời giải?

Dưới đây là các đề toán thực tế ôn thi tuyển sinh 10 năm 2025 có lời giải?

Đề toán thực tế 1: Sau dịp Tết Nguyên đán, hai anh em bạn Hoàng có được số tiền mừng tuổi là 3,5triệu đồng; hai anh em nhờ mẹ gửi số tiền đó vào ngân hàng. Mẹ nói với Hoàng: “Sau hai năm nữa, các con sẽ được nhận về số tiền cả gốc và lãi là 4,235 triệu đồng”. Hỏi thời điểm Hoàng gửi tiền, lãi suất ngân hàng là bao nhiêu % trong một năm, biết rằng số tiền lãi sau năm thứ nhất sẽ được tính vào tiền gốc của năm thứ hai.

Lời giải

Gọi lãi suất của ngân hàng a (phần trăm), a > 0 

Số tiền lãi sau năm thứ nhất gửi là: 3,5a (triệu đồng)

Tổng số tiền đem gửi năm thứ hai là: 3,5 + 3,5a (triệu đồng)

Số tiền lãi sau năm thứ hai gửi là: (3,5 + 3,5a)a (triệ đồng)

Theo đề bài sau hai năm gửi tổng số tiền cả gốc và lãi mà anh em Hoàng có được là 4,235 triệu đồng, nên ta có phương trình:

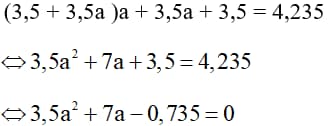
Giải phương trình tìm được a1 = 0,1 (TM); a2 = -2,1 (KTM)

Vậy lãi suất của ngân hàng là 10%

Đề toán thực tế 2: Dân số hiện nay của một phường là 40000 người. Sau 2 năm dân số của phường được dự tính là 41618 người. Hỏi mỗi năm dân số của phường tăng bao nhiêu phần trăm?

Lời giải

Gọi tỉ lệ tăng dân số của phương là x(%) (x > 0)

Sau 1 năm dân số của phường tăng lên là: 40000x (người)

Số dân của phường sau 1 năm là: 40000 + 40000x (người)

Sau 2 năm dân số của phường tăng lên là: (40000 + 40000x)x (người)

Mặt khác theo đề bài sau 2 năm dân số của phường tăng lên: 41618 – 40000 = 1618 (người)

Từ đó ta có phương trình: 

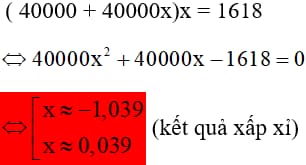
x ≈ 0,039 (thỏa mãn), x ≈ -1,039(không thỏa mãn)

Vậy tỉ lệ tăng dân số là 3,9%.

Đề toán thực tế 3: Một tháp nước có bể chứa là một hình cầu, đường kính bên trong của bể đo được là 6 mét. Người ta dự tính lượng nước đựng đầy trong bể đủ dùng cho một khu dân cư trong 5 ngày. Cho biết khu dân cư đó có 1304 người. Hỏi người ta đã dự tính mức bình quân mỗi người dùng bao nhiêu lít nước trong một ngày?

(Lấy 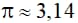 kết quả làm tròn đến chữ số thập phân thứ nhất)

Lời giải

Bán kính hình cầu của bể nước là: R = 6 : 2 = 3(m) 

Thể tích của bể nước hình cầu là:

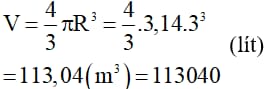
Lượng nước chứa đầy bể xấp xỉ 113040 lít nước

Lượng nước khu dân cư dùng trong 1 ngày là: 113040 : 5 = 22608(lít)

Đề toán thực tế 4: Ba đội máy cày làm việc trên ba cánh đồng có diện tích bằng nhau. Đội thứ nhất hoàn thành công việc trong 12 ngày, đội thứ hai hoàn thành công việc trong 9 ngày, đội thứ ba trong 8 ngày. Hỏi mỗi đội bao nhiêu máy cày? Biết tổng số máy cày của cả đội là 46 máy.

Lời giải

Gọi x,y,z lần lượt là số máy cày của đội thứ nhất, thứ hai, thứ ba. Do cùng một diện tích làm việc, số máy cày sẽ tỉ lệ nghịch với số ngày làm việc (số máy càng nhiều, ngày làm càng ít), từ đó suy ra 12x = 9y = 8z (theo giả thiết).

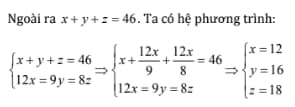
Vậy số máy cày của đội thứ nhất, thứ ha, thứ ba lần lượt là 12,16,18.

Đề toán thực tế 5: Ba vị khách cùng mướn 1 phòng tại khách sạn giá 30 USD. Người nhân viên đưa cho 3 vị khách hóa đơn 30 USD, thế nhưng sau đó anh ta mới nhận ra là mình đã tính nhầm. Thực ra giá phòng của họ chỉ tốn 25 USD mà thôi. Tuy nhiên, người nhân viên lại không biết làm thế nào để chia đều 5 USD cho 3 vị khách. Chính vì vậy anh quyết định chi trả cho mỗi người 1 USD và giữ cho mình 2 USD. Như vậy tổng cộng là 3 vị khách đã mất 27 USD trong khi người phục vụ giữ 2 USD cho mình. Vậy tổng cộng là 29 USD. Thế nhưng ban đầu 3 vị khách đưa cho phục vụ 30 USD, vậy 1 USD đã biến đi đâu mất?

Gợi ý giải

Tổng cộng 3 vị khách mất đi 27 USD là đúng vì ba vị khách chỉ nhận lại được 3 USD. Người phục vụ giữ 2 USD là đúng về mặt số liệu. Nhưng câu nói “tổng cộng là 29 USD" nghĩa là gộp 27 USD ba vị khách đã mất với 2 USD người phục vụ giữ, đây là phép tính sai vì 2 USD đó nằm trong số 27 USD mà ba vị khách mất đi: 27 USD 3 vị khách mất đi gồm 25 USD tiền phòng và 2 USD người phục vụ giữ vì không có tiền thối.

Vậy 1 USD không biến mất. Đây là cú lừa của đề bài.

Đề toán thực tế 6: Hai bạn An và Bình cùng mang một số tiền như nhau đến nhà sách để mua tập. An định mua loại tập gia 2.500đ/1 quyền. còn Bình mua loại tập giá 3000đ/1 quyền. khi đến nhà sách hai bạn mới biết các loại tập đều được giảm giá 20%. Vì thế số tập của bạn An mua được nhiều hơn số tập của bạn Bình là 10 quyển. Biết số tiền mà các bạn mang theo là vừa đủ để mua tập. Hỏi số tập mỗi bạn mua được và số tiền hai bạn mang theo là bao nhiêu?

Lời giải

Gọi a,b lần lượt là số tập mỗi bạn An và Bình mua

Gọi c là số tiền 2 bạn An và Bình mang theo

Các loại tập đều được giảm giá 20% nên ta có số tiền An và Bình dùng để mua tập lần lượt là (1-20%).2500a và (1-20%).3000b

Do cả hai đều dùng vừa đủ số tiền mang theo nên: c = 80%.2500a=80%.3000b => c = 2000a = 2400a

Số tập An mua được nhiều hơn số tập Bình mua 10 quyển: a - b = 10

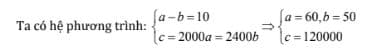
Lưu ý: Thông tin về đề toán thực tế và lời giải chỉ mang tính chât tham khảo!

Tổng hợp các đề toán thực tế ôn thi tuyển sinh 10 năm 2025 có lời giải? (Hình ảnh từ Internet)

Lịch thi tuyển sinh lớp 10 năm 2025 TPHCM diễn ra vào khi nào?

Theo thông tin chính thức, UBND TP.HCM đã có Quyết định 1186/QĐ-UBND năm 2025 về phê duyệt Kế hoạch huy động trẻ ra lớp và tuyển sinh vào các lớp đầu cấp năm học 2025 - 2026.

Trong đó, kế hoạch thi tuyển sinh vào lớp 10 TP.HCM năm học 2025 - 2026 như sau:

Lịch thi tuyển sinh lớp 10 TP.HCM năm học 2025 - 2026:

- Thời gian thi dự kiến: ngày 06 và 07/6/2025.

- Số môn thi, bài thi: gồm ba môn thi Toán, Ngữ văn (120 phút/môn), Ngoại ngữ (90 phút).

Kỳ thi tuyển sinh THPT được tổ chức mấy lần 1 năm?

Căn cứ Điều 9 Quy chế tuyển sinh Trung học cơ sở và tuyển sinh Trung học phổ thông ban hành kèm theo Thông tư 30/2024/TT-BGDĐT quy định về tổ chức thi tuyển sinh THPT như sau:

Phương thức tuyển sinh trung học phổ thông

1. Hằng năm tổ chức 01 (một) lần tuyển sinh trung học phổ thông.

2. Tuyển sinh trung học phổ thông được tổ chức theo 01 (một) trong 03 (ba) phương thức: xét tuyển, thi tuyển, kết hợp thi tuyển với xét tuyển.

a) Xét tuyển: căn cứ xét tuyển là kết quả rèn luyện và kết quả học tập các năm học theo chương trình giáo dục phổ thông cấp trung học cơ sở hoặc chương trình giáo dục thường xuyên cấp trung học cơ sở của đối tượng tuyển sinh, nếu lưu ban lớp nào thì lấy kết quả năm học lại của lớp đó.

b) Thi tuyển: thực hiện theo quy định tại Điều 13 Quy chế này.

c) Kết hợp thi tuyển với xét tuyển: thực hiện kết hợp theo quy định tại điểm a và điểm b của khoản này.

Theo quy định trên, kỳ thi tuyển sinh THPT sẽ được tổ chức 1 lần trong 1 năm theo quy định mới nhất.